3Dplaneのノウハウ

「ゴルフの幾何学」２．ボールを曲げてピンに寄せる　～その１

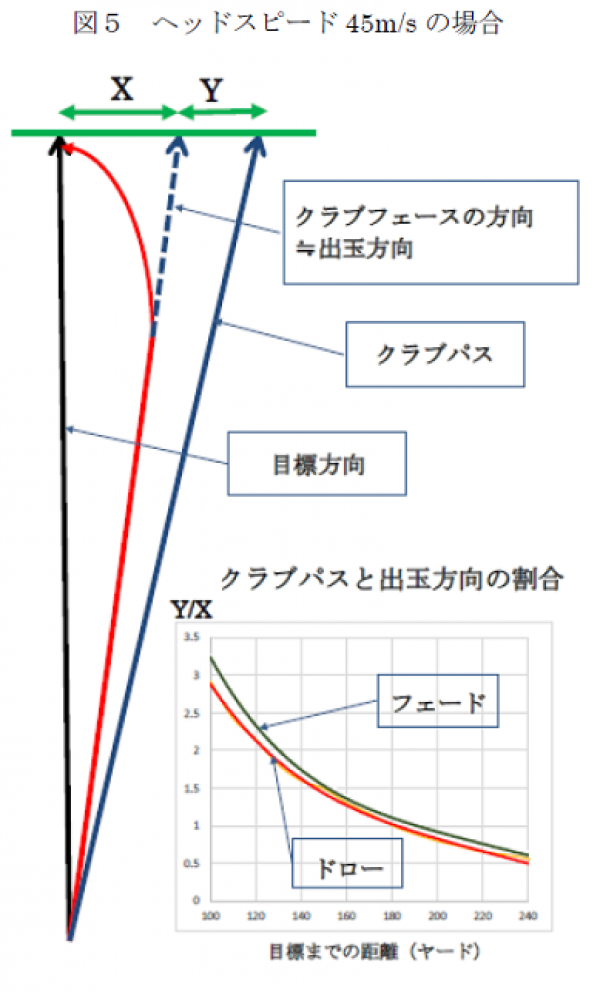
ボールを曲げてピンに寄せることは、簡単なことではありません。ボールを曲げることは、それほど難しいことではないのですが、その曲がり具合をコントロールすること、また飛距離やボールが落ちてからのランも考えるとボールを曲げてピンを狙うことは、非常に多くの要素を考慮しなければなりません。 まず、ボールが曲がる要素を考えると、横風とかフェースのスィートスポットから外れて打った場合、また前上がり等の傾斜地から打った場合等ありますが、ここでは、 D Plane理論によるスピン軸の傾き のみを考えます。 スピン軸の傾きは、クラブパスとフェースアングルの2つの方向の差異によって起ります。クラブパスよりフェースアングルが右に向いていれば、スピン軸は、右に傾き、ボールは、右に曲がって行きます。逆に場合、クラブパスよりフェースアングルが左に向いていれば、スピン軸は、左に傾いて、ボールは、左に曲がっていくのです。 フェースアングルとクラブパスの差をフェースツゥーパスと言います。 どうやって、フェースツゥーパスを作るのか、最も簡単なやり方は、グリップを変えてフェースを閉じたり開いたりして、一方スイングは、変えないで普通に真っすぐ振ることです。スイングを変えないでクラブパスを変えるには、アドレスの向きを変えれば良いのです。 　　アドレスの向きを変えないでクラブパスを変えるのは、スイングを変えることになり、ボールを正確に捕えることが、難しくなることが、考えられます。 ボールの出ていく方向（出玉方向）は、ほぼフェースの向きとなります。厳密には、アイアンでフェースツゥーパスの約70％と言われていますが、この割合は、フェース面の摩擦係数等で決まりますので、一般的には、決まりません。そこでここでは、出玉方向は、フェースの向きとなると考えます。 ドローボールの場合、ボールの出玉方向は、目標の右側で、左に曲がって目標に向かいます。フェードボールは、その反対にボールは、目標の左側に出て行き、右に曲がって行きます。 ボールが目標方向に行くには、クラブパスは、ドローボールの場合、ボールの出玉方向よりさらに右に向くことになります。クラブパスをどれほど右に向ければボールが目標方向に行くのか、それは、目標とボールの出玉方向の角度と目標までの距離、及びスピンロフトに関係します。 フェースアングルとクラブパスの差、つまりフェースツゥーパスが大きいとボールの曲がりも大きくなります。また、距離が長くなると滞空時間が長くなりますから、その分ボールの曲がり幅も大きくなります。 また、スピンロフトが小さくなるとバックスピンが少なくなりますが、するとスピン軸の傾きが大きくなります。スピン軸の傾きは、バックスピンと横方向のスピンの合成ですから、バックスピンだけ小さくなるとスピン軸の傾きが大きくなるのです。つまり、同じ距離でもロフトが小さなクラブで打つ方が、同じフェースツゥーパスでも曲がりが大きくなるのです。 目標までの距離、出玉方向及びスピンロフトが決まれば、目標近くに着弾するためのクラブパスが求められます。 出玉方向とクラブパスの関係は、簡単な式では、表せず、上図のようになります。出玉方向（目標からの横方向距離）をX、出玉方向とクラブパスの方向をYとすると、その比Y/Xは、ドライバーのヘッドスピードが45m/sの場合、右下のクラブのようなカーブになります。

最終更新日：2021-03-29 05:07:10

3Dplaneのノウハウ一覧