3Dplaneのノウハウ

「ゴルフの幾何学」２．ボールを曲げてピンに寄せる　～その２

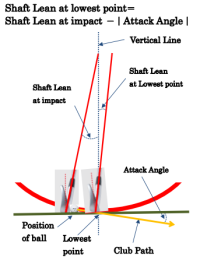
ドローとフェードでは、ドローはフェースをクローズにし、フェードは、フェースをオープンにすることになり、ドローを打つ方が、ロフトが小さくなるので、フェースツゥーパスも小さくなります。また、ヘッドスピードが速いプレーヤーは、同じ距離をより大きなロフトのクラブで打つことになるので、フェースツゥーパスが全体に大きくなります。 例えば、ピンまでの距離を100ヤード、出玉方向をピンの右5ヤードとすると、グラフよりY/Xが約3ですから、クラブパスは、出玉方向よりさらに約15ヤードピンの右に向ければ、ピン方向に行くことになります。ピンまでの距離が150ヤード、出玉方向を同じく右5ヤードとすると、Y/Xが約1.5ですからクラブパスは、出玉方向の右約7.5ヤードとなります。ピンまでの距離200ヤードで同条件の時は、Y/Xが約0.8で、クラブパスは、出玉方向の右約4ヤードとなります。 フェードボールで目標を狙う場合、距離が150ヤード、出玉方向を左5ヤードとすると、Y/Xが約1.6ですからクラブパスは、出玉方向の左約8ヤードとなります。出玉方向を左10ヤードとすると、クラブパスは、出玉方向の左16ヤードとなります。この場合、クラブフェースを約6度オープンにすることになります。すると約2度ロフトが多くなります。すると約半番手飛ばないことになりますので、1番手上げるとロフトがその分少なくなるので、計算するとY/Xが約1.5になり、クラブパスは、出玉方向の左15ヤードとなります。 フェースツゥーパス を変化させて打つ場合、フェースをクローズまたはオープンにして打つことになりますが、そうするとロフトが変わります。すると飛距離が変わってきます。計算に必要なフェースアングルの変化は、次式になります。 フェースアングルの変化=tan^(-1)⁡((X＋Y)/目標までの距離)-tan^(-1) (X/目標までの距離) 前出のピンまでの距離を100、150、200ヤードで出玉方向をピンの右５ヤードとすると、フェースアングルの変化は、それぞれ約8.5度、約2.9度、約1.2度になります。 後述で説明しますが、ライ角を65度とするとフェースアングル8.5度の変化は、約4度ロフトが変化します。4度と言うと9番アイアンとピッチング・ウェッジのロフト差が5度位ですから、約1番手変化します。ドローボールの場合、1番手分飛ぶと考えてショットしないといけません。150ヤードの時は、ロフトの変化は、約1.5度になります。番手間のロフト差は、だいたい4度位ですので、この場合も3分の1番手変化することになります。200ヤードの場合は、ロフトの変化は、約0.7度ですが、200ヤード飛ぶクラブの番手間のロフト差は、約2度になりますから、約3分の1番手分飛距離が変わることを考えてショットしないといけません。 以上をまとめると上表になります。 このようにボールを左右に曲げて目標を狙うことは、もの凄く難しいのです。プロレベルのゴルファーは、膨大な練習によって、ボールの曲がり量、目標までの距離から瞬時にどこを向いて、どうスイングしたら目標方向に行くかが分かるのでしょう。しかし、そのレベルを目指すジュニアゴルファーやアマチュアの上級者は、計算で求めたクラブパスやロフト変化からどうスイングするべきか知ってそれを目標にして練習することが上達の早道になると思われます。コーチやレッスンプロも単にドロー・フェードの打ち方を教えるのではなく、どうやったらボールを曲げてピンに寄せることが出来るのか数値を示して教えるべきと思います。

最終更新日：2022-12-01 14:49:17

3Dplaneのノウハウ一覧